MINN: Learning the dynamics of differential-algebraic equations and application to battery modeling

The concept of integrating physics-based and data-driven approaches has become popular for modeling sustainable energy systems. However, the existing literature mainly focuses on the data-driven surrogates generated to replace physics-based models. These models often trade accuracy for speed but lack the generalizability, adaptability, and interpretability inherent in physics-based models, which are often indispensable in modeling real-world dynamic systems for optimization and control purposes. We propose a novel machine learning architecture, termed model-integrated neural networks (MINN), that can learn the physics-based dynamics of general autonomous or non-autonomous systems consisting of partial differential-algebraic equations (PDAEs). The obtained architecture systematically solves an unsettled research problem in control-oriented modeling, i.e., how to obtain optimally simplified models that are physically insightful, numerically accurate, and computationally tractable simultaneously. We apply the proposed neural network architecture to model the electrochemical dynamics of lithium-ion batteries and show that MINN is extremely data-efficient to train while being sufficiently generalizable to previously unseen input data, owing to its underlying physical invariants. The MINN battery model has an accuracy comparable to the first principle-based model in predicting both the system outputs and any locally distributed electrochemical behaviors but achieves two orders of magnitude reduction in the solution time.

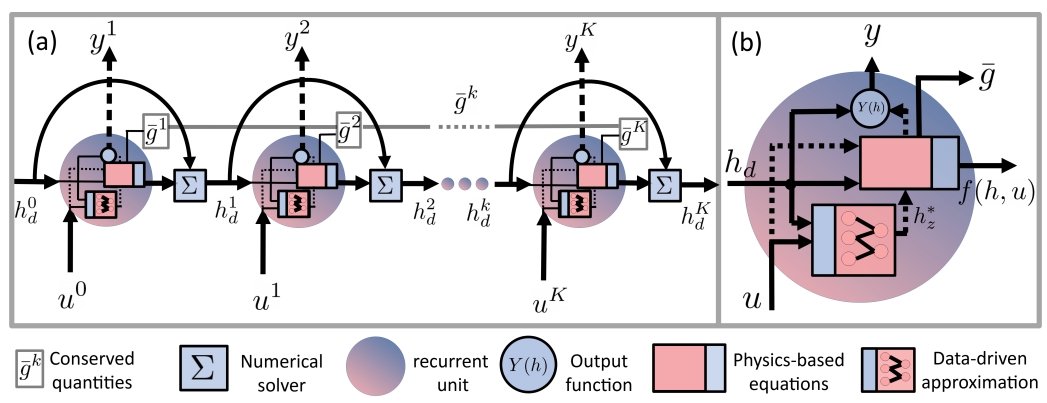Fig. 2. The proposed MINN architecture for dynamic systems. (a) An iterative update of the hidden states $h^k_d$, output $y_k$ and conserved quantities $g^k$, is controlled by input $u^k = u(t^k)$ at time $t^k$ through physics-based hidden units. This update is handled by the time integration via the numerical solver. (b) The design of a physics-based recurrent unit contains physics-based equations, a deep learning-enabled approximation (5) and an output function $Y$.

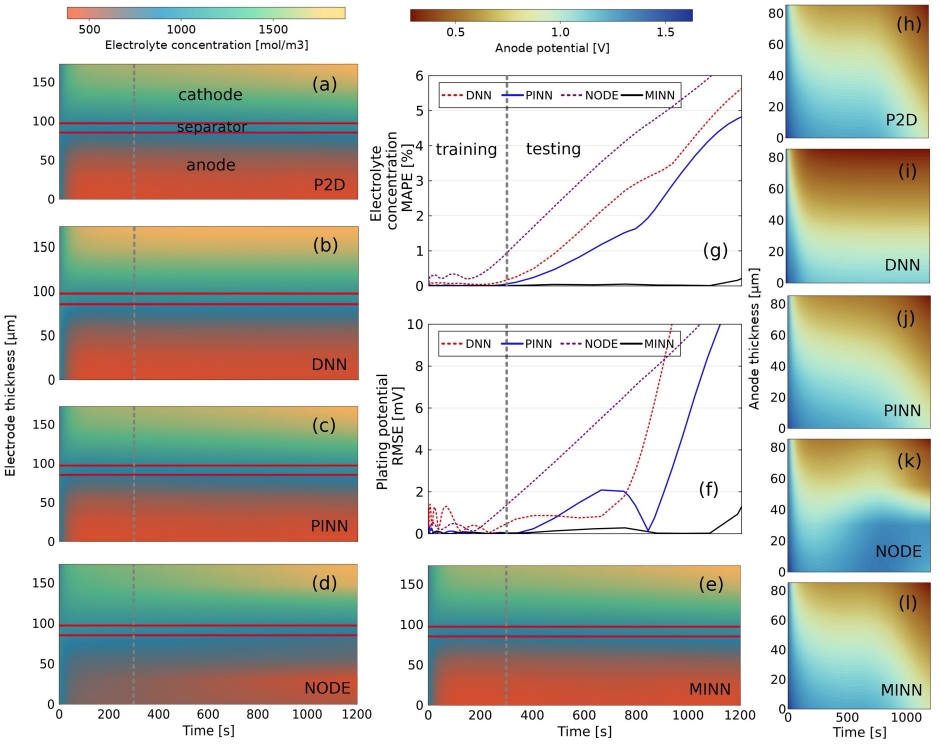Fig. 5. Comparison of different data-driven and hybrid model predictions under 1C charge with P2D predictions as ground truth. All four models are trained using data sampled from the first 300 seconds of the 1C charge data starting from 30% SOC. (a)–(e) Spatiotemporal plots of electrolyte concentration. (f) The mean absolute percentage error of electrolyte concentration averaged over the thickness. (g) The root mean square error of the plating potential averaged over the thickness. (h)-(l) Spatiotemporal plots of anode potential $\phi_s − \phi_e$.

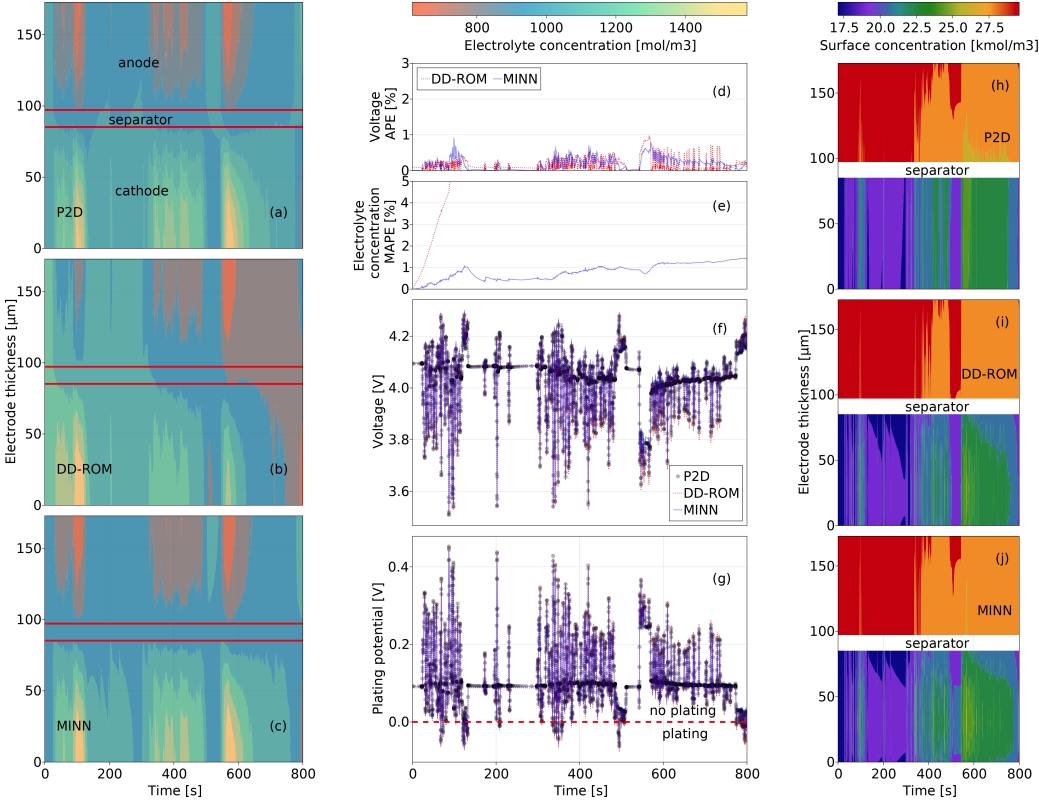Fig. 7. Performance of the DD-ROM and MINN battery models in learning system dynamics, compared with the results of reference 144-order P2D model. (a)-(c) Liquid-phase ion concentration (electrolyte concentration). (d)-(e) Generalization errors of terminal voltage and electrolyte concentration. (f) Terminal voltage response to the testing current. (g) Anode plating potential at the anode-separator interface. (h)-(j) Solid-phase concentration at the surface of particles.