线性二次调节器 Linear Quadratic Regulator (LQR)
Yang Li
Published:
线性二次型调节器(Linear quadratic regulator, LQR)是一种经典的最优控制方法,旨在对线性系统设计状态反馈控制律,使系统在满足稳定性的前提下最小化一个包含状态和控制输入加权的性能指标函数。通过求解不同形式的黎卡提(Riccati)方程,LQR 可以系统地权衡控制性能与能耗,实现稳健、平滑的系统响应,广泛应用于自动控制和现代控制系统设计中。
1. 无限时间区间连续时间型 LQR
考虑如下连续时间线性时不变系统
\[\dot{\mathbf{x}}(t) = f(\mathbf{x}(t), \mathbf{u}(t)) = \mathbf{A} \mathbf{x}(t) + \mathbf{B} \mathbf{u}(t), \quad \mathbf{x}(0) = \mathbf{x}_0\]其中:
- $\mathbf{x}(t) \in \mathbb{R}^n$:状态向量(State vector)
- $\mathbf{u}(t) \in \mathbb{R}^m$:控制输入(Control input)
- $f: \mathbb{R}^n \times \mathbb{R}^m \rightarrow \mathbb{R}^n$:动态系统函数
对于任意的初始状态 $\mathbf{x}(0)$,我们希望通过调节控制输入 $\mathbf{u}(t)$ 使系统状态回到原点。若系统可控,可以通过状态反馈实现:
\[\mathbf{u}(t) = - \mathbf{K} \mathbf{x}(t)\]其中:
- $\mathbf{K} \in \mathbb{R}^{m \times n}$:状态反馈增益(State feedback gain)
有多种经典的方法可以确定 $\mathbf{K}$,例如极点配置法(MATLAB 函数 place)。
LQR 是通过最优控制的方法确定 $\mathbf{K}$。对于无限时间区间连续时间型 LQR,其控制目标是最小化以下折扣型(Discounted)泛函–积分型代价函数(Cost function):
\[\begin{align} J &= \int_0^\infty e^{-\rho t} \ell(\mathbf{x}(t), \mathbf{u}(t)) dt \nonumber \\ &=\int_0^\infty e^{-\rho t}\left[ \mathbf{x}(t)^\top \mathbf{Q} \mathbf{x}(t) + \mathbf{u}(t)^\top \mathbf{R} \mathbf{u}(t) \right] dt \end{align}\]其中:
- \(\ell: \mathbb{R}^n \times \mathbb{R}^m \rightarrow \mathbb{R}\):运行成本(Running cost)。
- \(\rho>0\) :折扣因子(Discount factor)。
- $ \mathbf{Q} \in \mathbb{R}^{n \times n} $:状态权重矩阵(State weighting),对称半正定矩阵($ \mathbf{Q} \succeq 0 $),用于惩罚状态偏离。
- $ \mathbf{R} \in \mathbb{R}^{m \times m} $:输入权重矩阵(Input weighting),对称正定矩阵($ \mathbf{R} \succ 0 $),用于惩罚控制能量。
✅ 最优控制律(利用 HJB 推导)
推导最优控制率的过程如下。
首先,定义代价函数的最小值为值函数(Value Function, Critic):
\[V(\mathbf{x}) = \inf_{\mathbf{u}} J(\mathbf{x},\mathbf{u}) = \inf_{\mathbf{u}}\int_0^\infty e^{-\rho t} \left[ \mathbf{x}(t)^\top \mathbf{Q} \mathbf{x}(t) + \mathbf{u}(t)^\top \mathbf{R} \mathbf{u}(t) \right] dt\] \[\color{blue}{V(\mathbf{x}) = \inf_{\mathbf{u}} J(\mathbf{x},\mathbf{u}) = \inf_{\mathbf{u}} \int_0^\infty e^{-\rho t} \ell(\mathbf{x}(t), \mathbf{u}(t)) dt} \nonumber\]利用动态规划原理,得到无限时间区间的哈密顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman, HJB)方程:
\[\rho V(\mathbf{x}) = \min_{\mathbf{u}(t)} \left[\mathbf{x}^\top \mathbf{Q} \mathbf{x} +\mathbf{u}(t)^\top \mathbf{R} \mathbf{u}(t) + \nabla_{\mathbf{x}}V(\mathbf{x})^{\top} \cdot (\mathbf{A} \mathbf{x}(t) + \mathbf{B} \mathbf{u}(t)) \right] \label{eq:hjb1}\] \[\color{blue}{\rho V(\mathbf{x}) = \min_{\mathbf{u}(t)} \left[ \ell(\mathbf{x}(t), \mathbf{u}(t)) + \nabla_{\mathbf{x}}V(\mathbf{x})^{\top} \cdot f(\mathbf{x},\mathbf{u}) \right]} \nonumber\]上式右侧取最小值时,根据最优性条件有:
\[2 \mathbf{R} \mathbf{u}(t) + \mathbf{B}^{\top} \nabla_{\mathbf{x}}V(\mathbf{x}) = 0 \label{eq:optimality1}\]可以证明,值函数为二次型:
\[V(\mathbf{x}) = \mathbf{x}(t)^{\top} \mathbf{P} \mathbf{x}(t)\]其中 $\mathbf{P} \in \mathbb{R}^{n \times n}$ 是一对称常值变换方阵。因此:
\[\nabla_{\mathbf{x}}V(\mathbf{x}) = 2 \mathbf{P} \mathbf{x}(t) \label{eq:gradient_Vx1}\]将 \(\eqref{eq:gradient_Vx1}\) 带入 \(\eqref{eq:optimality1}\) 可得 LQR 的最优控制率或策略(Policy):
\[\begin{align} \mathbf{u}^*(t) &= \pi(\mathbf{x}) = - (\mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P}) \mathbf{x}(t) \label{eq_optu3} \end{align}\]在该最优轨迹下, HJB 方程变为:
\[\mathbf{x}^\top \mathbf{Q} \mathbf{x} +\mathbf{u}^{*\top} \mathbf{R} \mathbf{u}^* + (2 \mathbf{P} \mathbf{x})^{\top} \cdot (\mathbf{A} \mathbf{x} + \mathbf{B} \mathbf{u}^*) - \rho \mathbf{x}^{\top} \mathbf{P} \mathbf{x}=0\]带入最优控制率 \(\eqref{eq_optu3}\),可得到带有折扣的连续时间代数 Riccati 方程(Continuous-time algebraic Riccati equation, CARE):
\[\boxed{ \mathbf{A}^\top \mathbf{P} + \mathbf{P} \mathbf{A} - \mathbf{P} \mathbf{B} \mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P} + \mathbf{Q} - {\color{red} \rho \mathbf{P}} = \mathbf{0} } \label{eq:care}\]求解上式得到 $\mathbf{P}$ 后,带入 \(\eqref{eq_optu3}\) 便得完整的最优控制率。
可以看出该最优控制是状态反馈控制的一个特例,其中反馈增益为:
\[\begin{align} \mathbf{K} &= \mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P} \end{align}\]注意:对于时间无限的问题,控制率通常是时不变(Time-invariant)的。
可以证明,令 \(\tilde{\mathbf{A}} = \mathbf{A} - \frac{\rho}{2} \mathbf{I}\),有折扣的 Riccati 方程可以等价为一个标准的 CARE:
\[\boxed{ \tilde{\mathbf{A}}^\top \mathbf{P} + \mathbf{P} \tilde{\mathbf{A}} - \mathbf{P} \mathbf{B} \mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P} + \mathbf{Q} = \mathbf{0} }\]在 MATLAB 中,可以调用 care 或 icare(implicit CARE)函数计算出 $\mathbf{P}$:
[P, L, G] = icare(A_tilde, B, Q, R); % MATlAB 推荐使用 icare 取代 care
K = (R \ (B' * P));
或者用 lqr 函数直接得到控制增益 $\mathbf{K}$
[K, P, eigVals] = lqr(A_tilde, B, Q, R);
✅ 最优控制律(利用 PMP 推导)
\[\mathcal{H}(\mathbf{x}, \mathbf{u}, \boldsymbol{\lambda}, t) = e^{-\rho t} (\mathbf{x}^{\top} \mathbf{Q} \mathbf{x} + \mathbf{u}^{\top} \mathbf{R} \mathbf{u}) + \boldsymbol{\lambda}^{\top} (\mathbf{A} \mathbf{x} + \mathbf{B} \mathbf{u}) \label{eq_hamiltonian}\] \[\color{blue}{\mathcal{H}(\mathbf{x}, \mathbf{u}, \boldsymbol{\lambda}, t) = e^{-\rho t} \ell(\mathbf{x}(t), \mathbf{u}(t)) + \boldsymbol{\lambda}^{\top} f(\mathbf{x}(t), \mathbf{u}(t))} \nonumber\]其中 $\boldsymbol{\lambda} \in \mathbb{R}^n$ 是协态(Costate)。在最优控制的条件下,\(\mathbf{x} = \mathbf{x}^*, \mathbf{u} = \mathbf{u}^*\),对应的一阶条件(First-order conditions, FOC)为:
- 状态方程:
- 协态方程:
- 最优性条件(Optimality condition):
利用最优性条件 \(\eqref{eq:optimality}\) 可得 LQR 的最优控制率:
\[\begin{align} \mathbf{u}^*(t) &= -\frac{1}{2} e^{\rho t} \mathbf{R}^{-1} \mathbf{B}^{\top} \boldsymbol{\lambda}(t) = - (\mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P}) \mathbf{x}(t) \end{align}\]其中:
\[\boldsymbol{\lambda}(t) = 2 e^{-\rho t} \mathbf{P} \mathbf{x}(t)\]为了求得 \(\mathbf{P}\),将上式带入协态方程 \(\eqref{eq:costate_eq}\),得:
\[2 e^{-\rho t} \mathbf{P} \dot{\mathbf{x}}(t) -2 e^{-\rho t} \rho \mathbf{P} \mathbf{x}(t) = - 2 e^{-\rho t}\mathbf{Q} \mathbf{x}(t) - 2 e^{-\rho t}\mathbf{A}^{\top} \mathbf{P} {\mathbf{x}}(t)\]即
\[\mathbf{P} \dot{\mathbf{x}}(t) = - \mathbf{Q} \mathbf{x}(t) - \mathbf{A}^{\top} \mathbf{P} {\mathbf{x}}(t) + \rho \mathbf{P} \mathbf{x}(t)\]并结合状态方程 \(\eqref{eq:state_eq}\),得: \(\mathbf{P} [\mathbf{A} \mathbf{x}(t) + \mathbf{B} \mathbf{u}(t)] = -\mathbf{Q} \mathbf{x}(t) - \mathbf{A}^{\top} \mathbf{P} {\mathbf{x}}(t) + \rho \mathbf{P} \mathbf{x}(t)\)
再把 \(\eqref{eq_optu3}\) 带入上式,得:
\[\mathbf{P} [\mathbf{A} \mathbf{x}(t) - \mathbf{B} (\mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P}) \mathbf{x}(t)] = -\mathbf{Q} \mathbf{x}(t) - \mathbf{A}^{\top} \mathbf{P} {\mathbf{x}}(t)+ \rho \mathbf{P} \mathbf{x}(t)\]消调 \(\mathbf{x}(t)\) 并整理,可得到带有折扣的连续时间代数 Riccati 方程 \(\eqref{eq:care}\)。
✅ 最优控制律(利用 PMP 推导,构造协态变换)
定义一个协态变换:
\[\tilde{\boldsymbol{\lambda}} = e^{\rho t}\boldsymbol{\lambda} =\nabla V_{\mathbf{x}}(\mathbf{x})\]构造一个新的 Hamiltonian:
\[\tilde{\mathcal{H}}(\mathbf{x},\mathbf{u},\tilde{\boldsymbol{\lambda}}) = (\mathbf{x}^{\top} \mathbf{Q} \mathbf{x} + \mathbf{u}^{\top} \mathbf{R} \mathbf{u}) + \tilde{\boldsymbol{\lambda}}^{\top} (\mathbf{A} \mathbf{x} + \mathbf{B} \mathbf{u})\] \[\color{blue}{\tilde{\mathcal{H}}(\mathbf{x},\mathbf{u},\tilde{\boldsymbol{\lambda}}) = \ell(\mathbf{x}(t), \mathbf{u}(t)) + \tilde{\boldsymbol{\lambda}}^{\top} f(\mathbf{x}(t), \mathbf{u}(t))} \nonumber\]协态方程变为:
\[\dot{\tilde{\boldsymbol{\lambda}}} = -2 \mathbf{Q} \mathbf{x} - \mathbf{A}^{\top} \tilde{\boldsymbol{\lambda}} +\rho \tilde{\boldsymbol{\lambda}}\] \[\color{blue}{\dot{\tilde{\boldsymbol{\lambda}}} = -\frac{\partial \tilde{\mathcal{H}}}{\partial \mathbf{x}} + \rho \tilde{\boldsymbol{\lambda}} = -\frac{\partial \ell}{\partial \mathbf{x}} - \left(\frac{\partial f}{\partial \mathbf{x}} \right )^{\top} \tilde{\boldsymbol{\lambda}} + \rho \tilde{\boldsymbol{\lambda}}} \nonumber\]最优性条件:
\[\frac{\partial \tilde{\mathcal{H}}}{\partial \mathbf{u}} = 2 \mathbf{R} \mathbf{u}(t) + \mathbf{B}^{\top} \tilde{\boldsymbol{\lambda}}(t) = 0\] \[\color{blue}{\frac{\partial \tilde{\mathcal{H}}}{\partial \mathbf{u}} = \frac{\partial \ell}{\partial \mathbf{u}} + \left(\frac{\partial f}{\partial \mathbf{u}} \right )^{\top} \tilde{\boldsymbol{\lambda}} = 0 }\nonumber\]根据:
\[\begin{align} V(\mathbf{x}) &= \mathbf{x}^{\top} \mathbf{P} \mathbf{x}\\ \tilde{\boldsymbol{\lambda}} &= \nabla V_{\mathbf{x}}(\mathbf{x}) = 2 \mathbf{P} \mathbf{x} \end{align}\]最终可推导出 \(\eqref{eq:care}\)。
✅ Q 函数
由 HJB 方程得:
\[0 = \min_{\mathbf{u}(t)} \left[ \ell(\mathbf{x}(t), \mathbf{u}(t)) + \nabla_{\mathbf{x}}V(\mathbf{x})^{\top} \cdot f(\mathbf{x},\mathbf{u}) - \rho V(\mathbf{x}) \right] \nonumber \\\]1) HJB-Residual Q(DP-Residual Q) 定义:
\[\begin{align} \mathcal{Q}_{\text{res}}(\mathbf{x},\mathbf{u}) &= \tilde{\mathcal{H}}(\mathbf{x},\mathbf{u},\nabla_{\mathbf{x}}(\mathbf{x})) - \rho V(\mathbf{x}) \nonumber \\ &= \ell(\mathbf{x}(t), \mathbf{u}(t)) + \nabla_{\mathbf{x}}(\mathbf{x})^{\top} f(\mathbf{x}(t), \mathbf{u}(t)) - \rho V(\mathbf{x}) \nonumber \\ &= (\mathbf{x}^{\top} \mathbf{Q} \mathbf{x} + \mathbf{u}^{\top} \mathbf{R} \mathbf{u}) + \tilde{\boldsymbol{\lambda}}^{\top} (\mathbf{A} \mathbf{x} + \mathbf{B} \mathbf{u}) - \rho \mathbf{x}^{\top} \mathbf{P} \mathbf{x} \end{align}\]则有:
\[0 = \min_{\mathbf{u}(t)} \left[ \mathcal{Q}_{\text{res}}(\mathbf{x},\mathbf{u}) \right] \nonumber \\\]该定义下无法建立值函数和 Q 函数的迭代关系,通常不使用该种定义。
2) Bellman Q (DP Q)定义下,Q 等价于 Hamiltonian,即:
\[\begin{align} \mathcal{Q}_{\text{bell}}(\mathbf{x},\mathbf{u}) &= \tilde{\mathcal{H}}(\mathbf{x},\mathbf{u},\nabla_{\mathbf{x}}(\mathbf{x})) \\&= \ell(\mathbf{x}(t), \mathbf{u}(t)) + \nabla_{\mathbf{x}}(\mathbf{x})^{\top} f(\mathbf{x}(t), \mathbf{u}(t)) \nonumber \\ &= (\mathbf{x}^{\top} \mathbf{Q} \mathbf{x} + \mathbf{u}^{\top} \mathbf{R} \mathbf{u}) + \tilde{\boldsymbol{\lambda}}^{\top} (\mathbf{A} \mathbf{x} + \mathbf{B} \mathbf{u}) \end{align}\]则有 HJB 方程:
\[\rho V(\mathbf{x}) = \min_{\mathbf{u}(t)} \left[ \mathcal{Q}_{\text{bell}}(\mathbf{x},\mathbf{u}) \right] \nonumber \\\]即:
\[V(\mathbf{x}) = \frac{1}{\rho} \min_{\mathbf{u}(t)} \left[ \mathcal{Q}_{\text{bell}}(\mathbf{x},\mathbf{u}) \right] \nonumber \\\]线性系统下可以推导出:
\[\mathcal{Q}_{\text{bell}}(\mathbf{x},\mathbf{u}) =\begin{bmatrix}\mathbf{x}\\\mathbf{u}\end{bmatrix}^{\top} \underbrace{\begin{bmatrix}\mathbf{Q} + \mathbf{A}^\top \mathbf{P} + \mathbf{P} \mathbf{A} & \mathbf{P} \mathbf{B} \\ \mathbf{B}^\top \mathbf{P} & \mathbf{R} \end{bmatrix}}_{\mathbf{H}} \begin{bmatrix}\mathbf{x}\\\mathbf{u}\end{bmatrix}\]其中 \(\mathbf{H}\) 为 \(\mathcal{Q}_{\text{bell}}\) 的 Hessian 矩阵。记:
\[\mathbf{H} = \begin{bmatrix}\mathbf{Q} + \mathbf{A}^\top \mathbf{P} + \mathbf{P} \mathbf{A} & \mathbf{P} \mathbf{B} \\ \mathbf{B}^\top \mathbf{P} & \mathbf{R} \end{bmatrix} = \begin{bmatrix}\mathbf{H}_{xx} & \mathbf{H}_{xu} \\ \mathbf{H}_{ux} & \mathbf{H}_{uu} \end{bmatrix}\]Riccati 方程可以表示为:
\[\mathbf{H}_{xx} - \mathbf{H}_{xu} \mathbf{H}_{uu}^{-1} \mathbf{H}_{ux} = \rho \mathbf{P}\]连续时间系统的动态规划使用该定义。
3) 离散时间 Q 定义:考虑在一段时间 $\Delta t$ 内,记 \(\gamma = e^{-\rho t}\),定义 $Q$ 函数为:
\[\boxed{ \mathcal{Q}_{\Delta t}(\mathbf{x},\mathbf{u}) = \ell(\mathbf{x}(t), \mathbf{u}(t)) \Delta t + \gamma V(\mathbf{x}(t+\Delta t)) }\]展开可得:
\[\mathcal{Q}_{\Delta t}(\mathbf{x},\mathbf{u}) \approx V(\mathbf{x}) + \Delta t \left[ \ell(\mathbf{x}(t), \mathbf{u}(t)) + \nabla_{\mathbf{x}}(\mathbf{x})^{\top} f(\mathbf{x}(t), \mathbf{u}(t)) - \rho V(\mathbf{x}) \right]\]这时,
\[\min_{\mathbf{u}} \mathcal{Q}_{\Delta t}(\mathbf{x},\mathbf{u}) = V(\mathbf{x}) + \underbrace{\min_{\mathbf{u}} \left[ \ell(\mathbf{x}(t), \mathbf{u}(t)) + \nabla_{\mathbf{x}}(\mathbf{x})^{\top} f(\mathbf{x}(t), \mathbf{u}(t)) \right]}_{\rho V(\mathbf{x})} \Delta t - \rho V(\mathbf{x}) \Delta t= V(\mathbf{x})\]最后,利用 HJB 方程\(\eqref{eq:hjb1}\)可得:
\[\boxed{\min_{\mathbf{u}} \mathcal{Q}_{\Delta t}(\mathbf{x},\mathbf{u}) = V(\mathbf{x})}\]于是,得到贝尔曼方程(值函数迭代公式):
\[\boxed{ V(\mathbf{x}) = \min_{\mathbf{u}} \left[\ell(\mathbf{x}(t), \mathbf{u}(t)) \Delta t + \gamma V(\mathbf{x}(t+\Delta t)) \right] }\]以及 Q 函数迭代公式:
\[\boxed{\mathcal{Q}_{\Delta t}(\mathbf{x},\mathbf{u}) = \ell(\mathbf{x}(t), \mathbf{u}(t)) \Delta t + \gamma \min_{\mathbf{u}} \mathcal{Q}_{\Delta t}(\mathbf{x}(t+\Delta t),\mathbf{u}(t+\Delta t))}\]对于线性系统可以推导出 \(\mathcal{Q}_{\Delta t}\) 的解析表达式:
\[V(\mathbf{x}(t+\Delta t)) = \mathbf{x}(t+\Delta t)^\top \mathbf{P} \mathbf{x}(t+\Delta t)\] \[\begin{align} \mathbf{x}(t+\Delta t) &= (e^{\mathbf{A} \Delta t}) \mathbf{x}(t) + \left[\int_{t}^{t + \Delta t} e^{\mathbf{A} \Delta \tau} \mathbf{B} d \tau \right]\mathbf{u}(t) &(\text{Exact Discretization}) \nonumber \\ &= (e^{\mathbf{A} \Delta t}) \mathbf{x}(t) + \left[\mathbf{A}^{-1} (e^{\mathbf{A} \Delta \tau} - \mathbf{I}) \mathbf{B} \right]\mathbf{u}(t) &(\text{When } \mathbf{A} \text{ is invertible}) \nonumber \\ &\approx (\mathbf{I} + \mathbf{A} \Delta t) \mathbf{x}(t) + (\mathbf{B} \Delta t) \mathbf{u}(t) &(\text{First-Order Approximation}) \nonumber \\ & = \mathbf{A}_d \mathbf{x}(t) + \mathbf{B}_d \mathbf{u}(t) \end{align}\] \[\begin{align} \mathcal{Q}_{\Delta t}(\mathbf{x}, \mathbf{u}) &=\mathbf{x}^\top \mathbf{Q} \mathbf{x} + \mathbf{u}^\top \mathbf{R} \mathbf{u} + \gamma \mathbf{x}(t+\Delta t)^\top \mathbf{P} \mathbf{x}(t+\Delta t) \nonumber\\ &=\mathbf{x}^\top \mathbf{Q} \mathbf{x} + \mathbf{u}^\top \mathbf{R} \mathbf{u} + \gamma (\mathbf{A}_d \mathbf{x} + \mathbf{B}_d \mathbf{u})^\top \mathbf{P} (\mathbf{A}_d \mathbf{x}+ \mathbf{B}_d \mathbf{u}) \nonumber\\ &=\begin{bmatrix}\mathbf{x}\\\mathbf{u}\end{bmatrix}^{\top} \begin{bmatrix}\mathbf{Q} + \gamma\mathbf{A}_d^\top \mathbf{P} \mathbf{A}_d & \gamma\mathbf{A}_d^\top \mathbf{P} \mathbf{B}_d \\ \gamma\mathbf{B}_d^\top \mathbf{P} \mathbf{A}_d & \mathbf{R} + \gamma\mathbf{B}_d^\top \mathbf{P} \mathbf{B}_d \end{bmatrix} \begin{bmatrix}\mathbf{x}\\\mathbf{u}\end{bmatrix} \end{align}\]💻 MATLAB 仿真示例
% Infinite-Horizon Continuous-Time LQR Control Simulation
clear; clc;
% --------------------------------------
% 1. System definition (continuous-time)
% --------------------------------------
A = [0 1; -2 -3]; % State matrix
B = [0; 1]; % Input matrix
Q = eye(2); % State weighting
R = 1; % Input weighting
% --------------------------------------
% 2. Solve continuous-time LQR via CARE
% --------------------------------------
[K, P, eigVals] = lqr(A, B, Q, R); % Compute optimal feedback gain
disp('LQR feedback gain K:');
disp(K);
% --------------------------------------
% 3. Simulation setup
% --------------------------------------
x0 = [1; 0]; % Initial state
t_span = [0 10]; % Simulation time interval
% --------------------------------------
% 4. Define closed-loop system dynamics
% dx/dt = (A - B*K)*x
% --------------------------------------
A_cl = A - B * K; % Closed-loop system matrix
f = @(t, x) A_cl * x; % Anonymous function for ODE solver
% --------------------------------------
% 5. Simulate using ODE45
% --------------------------------------
[t, X] = ode45(f, t_span, x0); % Solve ODE
% --------------------------------------
% 6. Compute control input u(t) = -K * x(t)
% --------------------------------------
U = -X * K'; % Each row of X multiplied by -K
% --------------------------------------
% 7. Plot results
% --------------------------------------
figure;
subplot(2,1,1);
plot(t, X(:,1), 'r-', 'LineWidth', 2); hold on;
plot(t, X(:,2), 'b--', 'LineWidth', 2);
xlabel('Time t'); ylabel('State $x(t)$');
legend('$x_1$','$x_2$');
title('LQR Closed-Loop State Response');
grid on;
subplot(2,1,2);
plot(t, U, 'k-', 'LineWidth', 2);
xlabel('Time $t$'); ylabel('Control input $u(t)$');
title('LQR Control Input');
grid on;
仿真结果如下
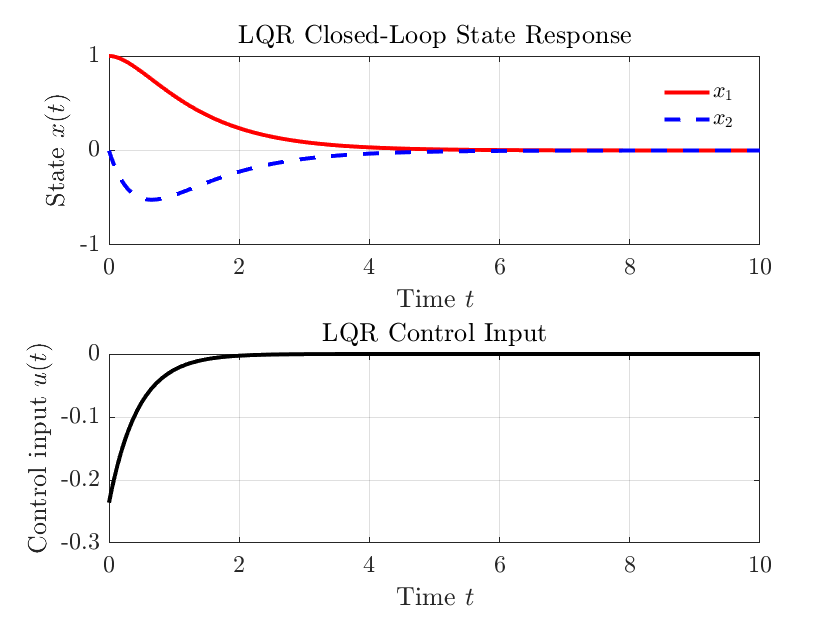
ChatGPT 问题:
- 连续时间代数 Riccati 方程有哪些解法?
- 在 LQR 控制中,反馈增益 $\mathbf{K}$ 是由 Riccati 方程中权重矩阵 $\mathbf{Q}$ 和 $\mathbf{R}$ 推导得到的。是否存在一个显式的数学表达式,能直接将 $\mathbf{Q}$、$\mathbf{R}$ 与闭环极点位置联系起来?或者,是否存在一种方法可以通过设定极点位置来反推合适的 $\mathbf{Q}$ 和 $\mathbf{R}$?
- 在 LQR 控制下,系统状态是否理论上可以在有限时间内完全达到零(并非无限接近 0)?如果不能,是不是永远也达不到零点?
2. 有限时间区间连续时间型 LQR
再次考虑连续时间线性时不变系统:
\[\dot{\mathbf{x}}(t) = \mathbf{A} \mathbf{x}(t) + \mathbf{B} \mathbf{u}(t), \quad \mathbf{x}(t_0) = \mathbf{x}_0\]其中:
- $\mathbf{x}(t) \in \mathbb{R}^n$:状态向量(State vector)
- $\mathbf{u}(t) \in \mathbb{R}^m$:控制输入(Control input)
控制目标变为最小化以下有限时间区间 \([ t_0, t_f ]\) 上的二次型性能指标:
\[J(\mathbf{x}_0,\mathbf{u}(t), t_0) = \mathbf{x}(t_f)^\top \mathbf{S} \mathbf{x}(t_f) + \int_{t_0}^{t_f} \left[ \mathbf{x}(t)^\top \mathbf{Q} \mathbf{x}(t) + \mathbf{u}(t)^\top \mathbf{R} \mathbf{u}(t) \right] dt\]其中:
$ \mathbf{Q} \succeq 0 $,状态惩罚矩阵(State penalty matrix)
$ \mathbf{R} \succ 0 $,控制惩罚矩阵(Control penalty matrix)
$ \mathbf{S} \succeq 0 $,终端惩罚矩阵(Terminal penalty matrix)
因此,在模型参数、惩罚矩阵、以及末端时间 \(t_f\) 确定的情况下,$J$ 的值由初始状态 \(\mathbf{x}_0\) 和控制轨迹 \(\mathbf{u}(t)\),以及初始时间 $ t_0 $ 唯一确定。
✅ 最优控制律
定义值函数(Value Function):
\[V(\mathbf{x}_0, t_0) = \min_{\mathbf{u}}{J(\mathbf{x}_0,\mathbf{u},t_0)}\]我们把 \(\mathbf{x}_0\) 和 \(t_0\) 看成变量,不妨分别用 \(\mathbf{x}\) 和 \(t\) 替代表示:
\[V(\mathbf{x}, t) = \min_{\mathbf{u}}{J(\mathbf{x},\mathbf{u},t)}\]上式对 \(t\) 求偏导,即得到连续时间的 HBJ 方程:
\[-\frac{\partial V(\mathbf{x}, t) }{\partial t} = \min_{\mathbf{u}(t)} \left[ \mathbf{x}^\top \mathbf{Q} \mathbf{x} + \mathbf{u}^\top \mathbf{R} \mathbf{u} + \nabla_{\mathbf{x}}V(\mathbf{x}, t)^{\top} \cdot (\mathbf{A} \mathbf{x} + \mathbf{B} \mathbf{u}) \right] \label{eq_hbj}\]且满足
\[V(\mathbf{x}, t_f) =\mathbf{x}^\top \mathbf{S} \mathbf{x}\]可以证明值函数为二次型函数结构:
\[V(\mathbf{x},t) = \mathbf{x}^\top \mathbf{P}(t) \mathbf{x}\]其中 $ \mathbf{P}(t) \in \mathbb{R}^{n \times n} $ 。
求 $V$ 的状态梯度:
\[\nabla_{\mathbf{x}}V = 2\mathbf{P}(t) \mathbf{x} \label{eq_dVdx}\]求 $V$ 的时间导数:
\[\frac{\partial V}{\partial t} = \mathbf{x}^\top \dot{\mathbf{P}}(t) \mathbf{x} \label{eq_dVdt}\]我们把 HBJ 方程 \(\eqref{eq_hbj}\) 等式的右边记为:
\[\min_{\mathbf{u}} \mathcal{H}(\mathbf{x},\mathbf{u},t) = \min_{\mathbf{u}} \left[\mathbf{x}^\top \mathbf{Q} \mathbf{x} + \mathbf{u}(t)^\top \mathbf{R} \mathbf{u}(t) + \nabla_{\mathbf{x}}V(\mathbf{x}, t)^{\top} \cdot (\mathbf{A} \mathbf{x}(t) + \mathbf{B} \mathbf{u}(t)) \right]\]这里的 \(\mathcal{H}\) 就是 \(\eqref{eq_hamiltonian}\) 中的 Hamiltonian。而对照 \(\eqref{eq_hamiltonian}\) 可知,等效的协态不仅和状态有关,还和时间有关:
\[\nabla V_{\mathbf{x}}(\mathbf{x},t) = 2\mathbf{P}(t) \mathbf{x} = \boldsymbol{\lambda}(\mathbf{x},t)\]将 \(\eqref{eq_dVdx}\) 和 \(\eqref{eq_dVdt}\) 带入上式,Hamiltonian 可写为:
\[\mathcal{H}(\mathbf{x},\mathbf{u},t) = \mathbf{x}^\top \mathbf{Q} \mathbf{x} + \mathbf{u}^\top \mathbf{R} \mathbf{u} + (\mathbf{P}(t) \mathbf{x})^{\top} \cdot (\mathbf{A} \mathbf{x} + \mathbf{B} \mathbf{u}))\]最优性条件:
\[\frac{\partial \mathcal{H}(\mathbf{x},\mathbf{u},t)}{\partial \mathbf{u}} = 0\]得到:
\[2\mathbf{R} \mathbf{u} + \mathbf{B}^\top \mathbf{P}(t) \mathbf{x} =0\]所以最优控制率具有状态反馈形式:
\[\mathbf{u}^*(\mathbf{x},t) = -\mathbf{K}(t) \mathbf{x} \label{eq_optu1}\]其中反馈增益为:
\[\mathbf{K}(t) = \mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P}(t) \label{eq_optu2}\]把 \(\eqref{eq_optu1}\) 和 \(\eqref{eq_optu2}\) 带入 HBJ 方程,可得到 Riccati 微分方程(Differential Riccati Equation):
\[\frac{d \mathbf{P}(t)}{dt} = -\mathbf{A}^\top \mathbf{P}(t) - \mathbf{P}(t) \mathbf{A} + \mathbf{P}(t) \mathbf{B} \mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P}(t) - \mathbf{Q}, \quad \mathbf{P}(t_f) = \mathbf{S} \label{eq:dre1}\]为了求解该Riccati 微分方程,需要从终端时间 $ t_f $ 向当前时间 $ t $ 反向进行,得到 $\mathbf{P}(t)$ 的轨迹,然后回带入最优控制率。
注意,和无限时长情况相比,有限时长情况下的反馈增益 \(\mathbf{K}\) 和变换矩阵 \(\mathbf{P}\) 都为时变矩阵。 考察有限时长和无限时长 LQR 的关系,可以看到当 $t_f \rightarrow \infty$ 时,可以去掉时间终端条件。此时 $\mathbf{P}(t)$ 的轨迹会收敛到一个稳态解 $\mathbf{P}_{\infty}$,满足下面的代数方程:
\[0 = -\mathbf{A}^\top \mathbf{P}_{\infty} - \mathbf{P}_{\infty} \mathbf{A} + \mathbf{P}_{\infty} \mathbf{B} \mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P}_{\infty} - \mathbf{Q}\]上式即是无限时长 LQR 问题中求解 $\mathbf{P}$ 的 CARE。
若取
\[\mathbf{S} = \mathbf{P}_{\infty}\]有限时长 LQR 等价于对应的无限时长 LQR 。此时 $\mathbf{P}(t) = \mathbf{P}_{\infty} $,而反馈增益 \(\mathbf{K}\) 也变为定值。
🔁 最优轨迹计算流程
求解 Riccati 微分方程
从 $ t_f $ 向 $ t_0 $ 反向求解 \(\eqref{eq:dre1}\),得到时变矩阵 $\mathbf{P}(t)$。
反馈增益计算
\[\mathbf{K}(t) = \mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P}(t)\]前向模拟系统状态
使用最优控制律:
\[\mathbf{u}^*(t) = -\mathbf{K}(t) \mathbf{x}(t)\]带入系统状态方程,求解系统状态轨迹 $\mathbf{x}(t)$。
💻 MATLAB 仿真示例
% Finite-Horizon Continuous-Time LQR Simulation
clear; clc;
% --------------------------------------
% 1. System definition (continuous-time)
% --------------------------------------
A = [0 1; -2 -3]; % State matrix
B = [0; 1]; % Input matrix
Q = eye(2); % State weighting
R = 1; % Input weighting
S = 10 * eye(2); % Terminal state cost matrix
t0 = 0; tf = 10; % Time interval
x0 = [1; 0]; % Initial state
% --------------------------------------
% 2. Solve Riccati Differential Equation backward in time
% --------------------------------------
% Convert matrix P to vector for ODE solver (column-stacked)
P_final = S;
p0 = reshape(P_final, [], 1); % Vectorize P(t_f)
% Riccati ODE: dP/dt = -A'*P - P*A + P*B*inv(R)*B'*P - Q
riccati_ode = @(t, p) ...
-reshape(A'*reshape(p,2,2) + reshape(p,2,2)*A ...
- reshape(p,2,2)*B*(R\B')*reshape(p,2,2) + Q, [], 1);
% Integrate backward in time
[t_back, p_sol] = ode45(riccati_ode, linspace(tf, t0, 100), p0);
% Flip time to increasing order
t_vec = flipud(t_back);
P_t = flipud(p_sol);
% Interpolate K(t) at arbitrary time
K_func = @(t) ...
(B' * reshape(interp1(t_vec, P_t, t, 'linear', 'extrap'), 2, 2)) / R;
% --------------------------------------
% 3. Define closed-loop dynamics with time-varying feedback
% dx/dt = (A - B*K(t)) * x
% --------------------------------------
f = @(t, x) (A - B * K_func(t)) * x;
% --------------------------------------
% 4. Simulate system dynamics
% --------------------------------------
[t_sim, X] = ode45(f, [t0 tf], x0);
% Compute u(t) = -K(t) * x(t)
U = zeros(length(t_sim),1);
for i = 1:length(t_sim)
Kt = K_func(t_sim(i));
U(i) = -Kt * X(i,:)';
end
% --------------------------------------
% 5. Plot results
% --------------------------------------
figure;
subplot(2,1,1);
plot(t_sim, X(:,1), 'r-', 'LineWidth', 2); hold on;
plot(t_sim, X(:,2), 'b--', 'LineWidth', 2);
xlabel('Time $t$'); ylabel('State $x(t)$');
legend('$x_1$','$x_2$');
title('Finite-Horizon LQR State Response');
grid on;
subplot(2,1,2);
plot(t_sim, U, 'k-', 'LineWidth', 2);
xlabel('Time $t$'); ylabel('Control input $u(t)$');
title('Finite-Horizon LQR Control Input');
grid on;
仿真结果如下
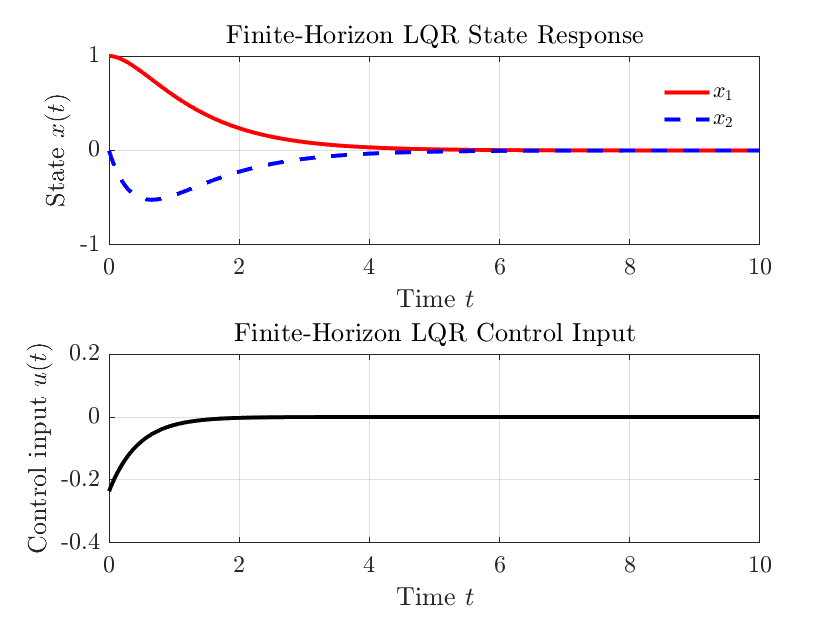
📌 与无限时间 LQR 对比
| 特性 | 有限时间 LQR | 无限时间 LQR |
|---|---|---|
| 控制律 | 时间相关:$ \mathbf{u}(t) = -\mathbf{K}(t) \mathbf{x}(t) $ | 常数反馈:$ \mathbf{u} = -\mathbf{K} \mathbf{x} $ |
| Riccati 方程 | 微分方程,需反向积分 | 代数方程(ARE) |
| 时间区间 | 固定区间 $[t_0, t_f]$ | 无限时间 |
| 稳定性设计 | 可调权重终端条件 $ \mathbf{S} $ | 设计即隐含稳定性 |
3. 无限时间长度离散时间型 LQR
考虑如下离散时间线性时不变系统
\[\mathbf{x}_{k+1} = \mathbf{A} \mathbf{x}_k + \mathbf{B} \mathbf{u}_k\]其中:
- $\mathbf{x}_k \in \mathbb{R}^n$:状态向量(State vector)
- $\mathbf{u}_k \in \mathbb{R}^m$:控制输入(Control input)
控制目标是将系统从任意初始值 $ \mathbf{x}_0 $ 带回原点。代价函数为
\[J = \sum_{k=0}^\infty \gamma^{i-k}\ell(\mathbf{x}_k,\mathbf{u}_k)= \sum_{k=0}^\infty \gamma^{i-k} \left( \mathbf{x}_k^\top \mathbf{Q} \mathbf{x}_k + \mathbf{u}_k^\top \mathbf{R} \mathbf{u}_k \right), \quad 0<\gamma\le 1\]其中:
- $ \mathbf{Q} \succeq 0 $:状态权重矩阵(State weighting)
- $ \mathbf{R} \succ 0 $:输入权重矩阵(Input weighting)
✅ 最优控制律
利用动态规划原理(Bellman Principle of Optimality),可以推导出其最优控制率,步骤如下。
首先,定义值函数(Value Function)为:
\[V(\mathbf{x}_k) = \min_{\{\mathbf{u}_k, \mathbf{u}_{k+1}, \dots\}} \sum_{i=k}^{\infty} \gamma^{i-k}\left( \mathbf{x}_i^\top \mathbf{Q} \mathbf{x}_i + \mathbf{u}_i^\top \mathbf{R} \mathbf{u}_i \right), \quad 0<\gamma\le 1\]显然,当 $k = 0$ 时,对应的值 $V(\mathbf{x}_0)$ 为最优控制对应的最小代价 $J$。
我们猜测(并稍后验证)值函数是一个二次型: \(V(\mathbf{x}_k) = \mathbf{x}_k^\top \mathbf{P} \mathbf{x}_k\)
其中 $\mathbf{P} \in \mathbb{R}^{n \times n}$ 是未知对称矩阵。
根据动态规划原理,有贝尔曼方程(Bellman Equation):
\[V(\mathbf{x}_k) = \min_{\mathbf{u}_k} \left[ \mathbf{x}_k^\top \mathbf{Q} \mathbf{x}_k + \mathbf{u}_k^\top \mathbf{R} \mathbf{u}_k + \gamma V(\mathbf{x}_{k+1}) \right]\]代入状态转移关系:
\[\mathbf{x}_{k+1} = \mathbf{A} \mathbf{x}_k + \mathbf{B} \mathbf{u}_k \Rightarrow V(\mathbf{x}_{k+1}) = (\mathbf{A} \mathbf{x}_k + \mathbf{B} \mathbf{u}_k)^\top \mathbf{P} (\mathbf{A} \mathbf{x}_k + \mathbf{B} \mathbf{u}_k)\]展开:
\[\begin{align} V(\mathbf{x}_k) = & \mathbf{x}_k^\top \mathbf{Q} \mathbf{x}_k + \mathbf{u}_k^\top \mathbf{R} \mathbf{u}_k + \gamma\mathbf{x}_k^\top \mathbf{A}^\top \mathbf{P} \mathbf{A} \mathbf{x}_k + 2 \gamma \mathbf{x}_k^\top \mathbf{A}^\top \mathbf{P} \mathbf{B} \mathbf{u}_k + \gamma\mathbf{u}_k^\top \mathbf{B}^\top \mathbf{P} \mathbf{B} \mathbf{u}_k \end{align}\]收集项后得到:
\[V(\mathbf{x}_k) = \mathbf{x}_k^\top (\mathbf{Q} + \gamma\mathbf{A}^\top \mathbf{P} \mathbf{A}) \mathbf{x}_k + \mathbf{u}_k^\top (\mathbf{R} + \gamma\mathbf{B}^\top \mathbf{P} \mathbf{B}) \mathbf{u}_k + 2 \gamma \mathbf{x}_k^\top \mathbf{A}^\top \mathbf{P} \mathbf{B} \mathbf{u}_k\]对右边关于 $ \mathbf{u}_k $ 求导,并令导数为 0,得:
\[2 (\mathbf{R} + \gamma\mathbf{B}^\top \mathbf{P} \mathbf{B}) \mathbf{u}_k + 2 \gamma \mathbf{B}^\top \mathbf{P} \mathbf{A} \mathbf{x}_k = 0\]于是得到解析算法:
\[\mathbf{u}_k = -\mathbf{K} \mathbf{x}_k, \quad \mathbf{K} = (\mathbf{R} + \gamma\mathbf{B}^\top \mathbf{P} \mathbf{B})^{-1} \gamma\mathbf{B}^\top \mathbf{P} \mathbf{A}\]其中 $\mathbf{P}$ 可以通过求解以下离散时间代数 Riccati 方程(discrete-time algebraic Riccati equation, DARE)得到(需要迭代求解):
\[\boxed{ \mathbf{P} = \mathbf{Q} + \gamma\mathbf{A}^\top \mathbf{P} \mathbf{A} -\gamma^2 \mathbf{A}^\top \mathbf{P} \mathbf{B} (\mathbf{R} + \gamma\mathbf{B}^\top \mathbf{P} \mathbf{B})^{-1} \mathbf{B}^\top \mathbf{P} \mathbf{A} }\]或者,令 \(\tilde{\mathbf{A}} = \sqrt{\gamma} \mathbf{A}\), \(\tilde{ \mathbf{B}} = \sqrt{\gamma} \mathbf{B}\),得到:
\[\boxed{ \mathbf{P} = \mathbf{Q} + \tilde{\mathbf{A}}^\top \mathbf{P} \tilde{\mathbf{A}} - \tilde{\mathbf{A}}^\top \mathbf{P} \tilde{\mathbf{B}} (\mathbf{R} + \tilde{\mathbf{B}}^\top \mathbf{P} \tilde{\mathbf{B}})^{-1} \tilde{\mathbf{B}}^\top \mathbf{P} \tilde{\mathbf{A}} }\]可以调用 dare 或 idare(implicit DARE)函数计算出 $\mathbf{P}$。
✅ Q 函数
Q 函数定义为(当前控制输入任意,以后所有的控制输入最优):
\[\begin{align} \mathcal{Q}(\mathbf{x}_k, \mathbf{u}_k) &= \ell(\mathbf{x}_k,\mathbf{u}_k) + \gamma V(\mathbf{x}_{k+1}) \nonumber \\ &=\mathbf{x}_k^\top \mathbf{Q} \mathbf{x}_k + \mathbf{u}_k^\top \mathbf{R} \mathbf{u}_k + \gamma V(\mathbf{x}_{k+1}) \nonumber\\ &=\begin{bmatrix}\mathbf{x}_k\\\mathbf{u}_k\end{bmatrix}^{\top} \begin{bmatrix}\mathbf{Q} + \gamma\mathbf{A}^\top \mathbf{P} \mathbf{A} & \gamma\mathbf{A}^\top \mathbf{P} \mathbf{B} \\ \gamma\mathbf{B}^\top \mathbf{P} \mathbf{A} & \mathbf{R} + \gamma\mathbf{B}^\top \mathbf{P} \mathbf{B} \end{bmatrix} \begin{bmatrix}\mathbf{x}_k\\\mathbf{u}_k\end{bmatrix} \end{align}\] \[V(\mathbf{x}_k) = \min_{\mathbf{u}_k} \mathcal{Q}(\mathbf{x}_k, \mathbf{u}_k)\]迭代法1:策略迭代(Policy Iteration)
通过迭代法求解 \(\mathbf{P}\) 和 \(\mathbf{K}\)
策略评估(Policy Evaluation):
\[\mathbf{P}^{(i+1)} = \mathbf{Q} + \mathbf{K}^{(i)\top} \mathbf{R} \mathbf{K}^{(i)} + \gamma(\mathbf{A} - \mathbf{B}\mathbf{K}^{(i)})^{\top}\mathbf{P}^{(i)}(\mathbf{A} - \mathbf{B}\mathbf{K}^{(i)})\]策略改进(Policy Improvement):
\[\mathbf{K}^{(i+1)} = (\mathbf{R} + \gamma\mathbf{B}^\top \mathbf{P}^{(i)} \mathbf{B})^{-1} \gamma\mathbf{B}^\top \mathbf{P}^{(i)} \mathbf{A}\]迭代法2:值函数迭代(Value Iteration)
利用上文 DARE 推导过程和结果进行迭代:
\[\mathbf{P}^{(i+1)} = \mathbf{Q} + \gamma\mathbf{A}^\top \mathbf{P}^{(i)} \mathbf{A} -\gamma^2 \mathbf{A}^\top \mathbf{P}^{(i)} \mathbf{B} (\mathbf{R} + \gamma\mathbf{B}^\top \mathbf{P} \mathbf{B})^{-1} \mathbf{B}^\top \mathbf{P}^{(i)} \mathbf{A}\]迭代法3:Q 函数迭代(Q-Iteration, Critic)
\[\mathcal{Q}(\mathbf{x}_k, \mathbf{u}_k) = \ell(\mathbf{x}_k,\mathbf{u}_k) + \gamma V(\mathbf{x}_{k+1})\] \[V(\mathbf{x}_{k+1}) = \min_{\mathbf{u}_{k+1}} \mathcal{Q}(\mathbf{x}_{k+1}, \mathbf{u}_{k+1})\]得到 Q 函数迭代公式:
\[\mathcal{Q}(\mathbf{x}_k, \mathbf{u}_k) =\ell(\mathbf{x}_k,\mathbf{u}_k)+ \gamma \min_{\mathbf{u}_{k+1}} \mathcal{Q}(\mathbf{x}_{k+1}, \mathbf{u}_{k+1})\]Q 函数对控制的导数:
\[\nabla_{\mathbf{u}} \mathcal{Q}(\mathbf{x}_k, \mathbf{u}_k) = 2 (\mathbf{R} + \gamma\mathbf{B}^\top \mathbf{P} \mathbf{B}) \mathbf{u}_k + 2 \gamma \mathbf{B}^\top \mathbf{P} \mathbf{A} \mathbf{x}_k\]💻 MATLAB 仿真示例
% Discrete-Time Infinite-Horizon LQR Simulation
clear; clc;
% --------------------------------------
% 1. System definition (discrete-time)
% --------------------------------------
A = [1 1; 0 1]; % State transition matrix
B = [0; 1]; % Input matrix
Q = eye(2); % State weighting matrix
R = 1; % Control weighting scalar
% --------------------------------------
% 2. Solve Discrete-Time Algebraic Riccati Equation (DARE)
% --------------------------------------
[K, P, eigVals] = dlqr(A, B, Q, R); % Compute LQR gain
disp('LQR gain K:');
disp(K);
% --------------------------------------
% 3. Simulation setup
% --------------------------------------
x = [2; 0]; % Initial state
N = 20; % Number of time steps
X = zeros(2, N+1); % State trajectory storage
U = zeros(1, N); % Control input storage
X(:,1) = x; % Set initial state
% --------------------------------------
% 4. Closed-loop simulation
% x_{k+1} = (A - B*K)*x_k
% --------------------------------------
for k = 1:N
u = -K * x; % Compute control input
x = A * x + B * u; % Apply closed-loop dynamics
X(:,k+1) = x; % Store new state
U(k) = u; % Store control input
end
% --------------------------------------
% 5. Plot results
% --------------------------------------
figure;
% Plot state trajectories
subplot(2,1,1);
plot(0:N, X(1,:), 'r-s', 0:N, X(2,:), 'b-*');
legend('$x_1$','$x_2$');
xlabel('Time step $k$');
ylabel('State $x_k$');
title('LQR Closed-Loop State Trajectory');
grid on;
% Plot control input
subplot(2,1,2);
stairs(0:N-1, U, 'k-', 'LineWidth', 2);
xlabel('Time step $k$');
ylabel('Control input $u_k$');
title('LQR Control Input');
grid on;
仿真结果如下
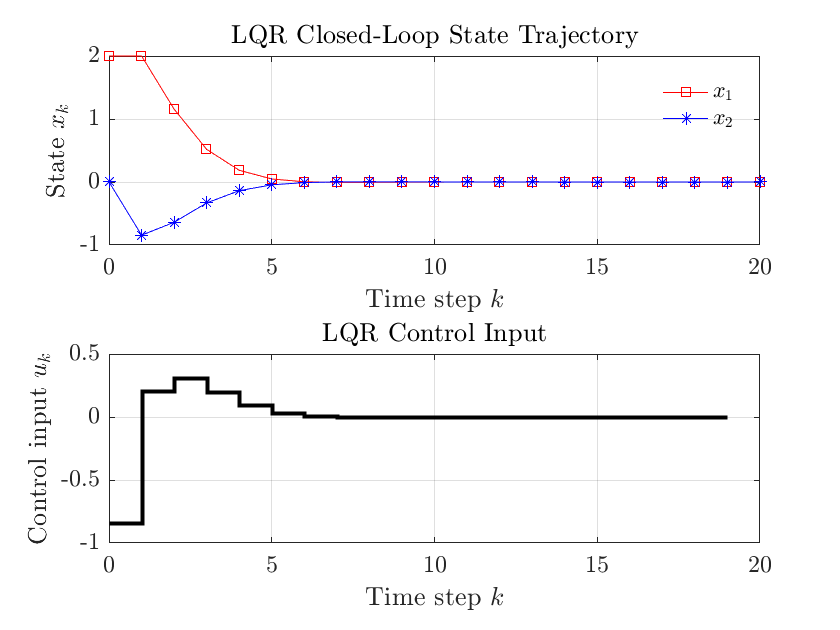
4. 有限时间长度离散时间型 LQR
考虑如下离散时间线性系统:
\[\mathbf{x}_{k+1} = \mathbf{A} \mathbf{x}_k + \mathbf{B} \mathbf{u}_k, \quad \mathbf{x}_0 \text{ 给定}\]控制目标是在有限时间区间内,最小化以下二次型性能指标:
\[J = \frac{1}{2} \mathbf{x}_N^\top \mathbf{S} x_N + \frac{1}{2} \sum_{k=0}^{N-1} \left( \mathbf{x}_k^\top \mathbf{Q} \mathbf{x}_k + \mathbf{u}_k^\top \mathbf{R} \mathbf{u}_k \right)\]其中:
- $ \mathbf{Q} \succeq 0 $:状态惩罚矩阵
- $ \mathbf{R} \succ 0 $:控制惩罚矩阵
- $ \mathbf{S} \succeq 0 $:终端状态惩罚矩阵
- $ N $:控制时间步长
✅ 最优控制律
该问题可以转化为一个标准的无约束二次规划(Quadratic Programming, QP)问题。其最优控制率具有如下形式:
\[\mathbf{u}_k = -\mathbf{K}_k \mathbf{x}_k\]其中反馈增益为:
\[\mathbf{K}_k = (\mathbf{R} + \mathbf{B}^\top \mathbf{P}_{k+1} \mathbf{B})^{-1} \mathbf{B}^\top \mathbf{P}_{k+1} \mathbf{A}\]📘 Riccati 递推公式
使用如下 向后递推的 Riccati 方程:
\[\mathbf{P}_k = \mathbf{Q} + \mathbf{A}^\top \mathbf{P}_{k+1} \mathbf{A} - \mathbf{A}^\top \mathbf{P}_{k+1} \mathbf{B} (\mathbf{R} + \mathbf{B}^\top \mathbf{P}_{k+1} \mathbf{B})^{-1} \mathbf{B}^\top \mathbf{P}_{k+1} \mathbf{A}\]终端条件为:
\[\mathbf{P}_N = \mathbf{S}\]🔁 算法流程
- 从 $ \mathbf{P}_N $ 开始向后迭代,计算每个时间步的 $ \mathbf{P}_k $
- 根据 $ \mathbf{P}_{k+1} $ 计算每个时间步的反馈增益 $ \mathbf{K}_k $
- 从 $ \mathbf{x}_0 $ 开始向前模拟系统轨迹,应用反馈律 $ \mathbf{u}_k = -\mathbf{K}_k \mathbf{x}_k $
📌 备注
- 控制器是随时间变化的(Time-varying)
- 当 $ N \to \infty $ 时,反馈增益 $ \mathbf{K}_k $ 可能收敛为定值
- 适用于轨迹规划、定时任务执行、终端状态设计等场景
- 没有不等式约束的模型预测控制(MPC)即为有限时间长度离散时间型 LQR
💻 MATLAB 仿真示例
% Finite-Horizon Discrete-Time LQR Simulation
clear; clc;
% --------------------------------------
% 1. System definition
% --------------------------------------
A = [1 1; 0 1]; % State transition matrix
B = [0; 1]; % Input matrix
Q = eye(2); % State cost
R = 1; % Control cost
S = 10 * eye(2); % Terminal state cost
N = 20; % Time horizon
x0 = [2; 0]; % Initial state
% --------------------------------------
% 2. Backward Riccati recursion
% --------------------------------------
P = cell(N+1,1); % Store P matrices
K = cell(N,1); % Store feedback gains
P{N+1} = S; % Terminal cost
for k = N:-1:1
Pk1 = P{k+1};
Kk = (R + B' * Pk1 * B) \ (B' * Pk1 * A);
K{k} = Kk;
P{k} = Q + A' * Pk1 * A - A' * Pk1 * B * Kk;
end
% --------------------------------------
% 3. Forward simulation with time-varying K_k
% --------------------------------------
X = zeros(2, N+1);
U = zeros(1, N);
x = x0;
X(:,1) = x;
for k = 1:N
u = -K{k} * x;
x = A * x + B * u;
X(:,k+1) = x;
U(k) = u;
end
% --------------------------------------
% 4. Plot results
% --------------------------------------
figure;
% State trajectories
subplot(2,1,1);
plot(0:N, X(1,:), 'r-s', 'LineWidth', 1); hold on;
plot(0:N, X(2,:), 'b-*', 'LineWidth', 1);
xlabel('Time step $k$'); ylabel('State');
legend('$x_1$','$x_2$');
title('Finite-Horizon LQR State Trajectory');
grid on;
% Control input
subplot(2,1,2);
stairs(0:N-1, U, 'k-', 'LineWidth', 2);
xlabel('Time step $k$'); ylabel('Control input $u_k$');
title('Finite-Horizon LQR Control Input');
grid on;
仿真结果如下
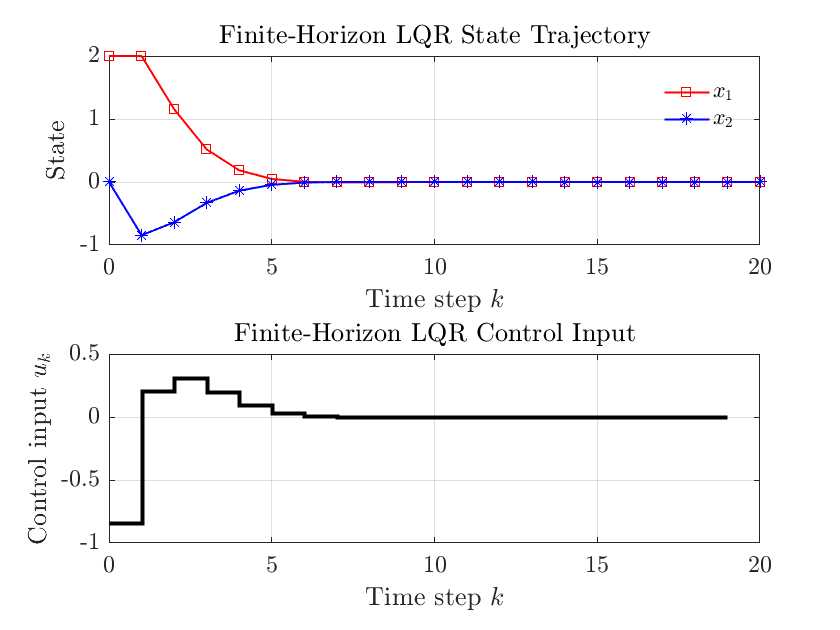
5. 跟踪型 LQR
Tracking LQR(跟踪型线性二次调节器) 是一种将标准 LQR 从调节扩展到轨迹跟踪的控制算法,其目标是使系统状态 $\mathbf{x}(t)$ 跟踪一个给定的参考轨迹 $\mathbf{x}_{\text{ref}}(t)$,同时最小化控制能量。
对于无限时间区间连续型 Tracking LQR,对应的代价函数(Cost function)为:
\[J = \int_0^\infty \left( (\mathbf{x}(t) - \mathbf{x}_{\text{ref}}(t))^\top \mathbf{Q} (\mathbf{x}(t) - \mathbf{x}_{\text{ref}}(t)) + \mathbf{u}(t)^\top \mathbf{R} \mathbf{u}(t) \right) dt\]其解为:
\[\begin{align} \mathbf{u}(t) &= - \mathbf{K} (\mathbf{x}(t) - \mathbf{x}_{\text{ref}}(t)) - \mathbf{R}^{-1} \mathbf{B}^{\top} \mathbf{s}(t) \\ \end{align}\]其中
\[\mathbf{K} = \mathbf{R}^{-1} \mathbf{B}^\top \mathbf{P}\]而 $\mathbf{s}(t)$ 满足下列的线性微分方程:
\[\dot{\mathbf{s}}(t) = -(\mathbf{A} - \mathbf{B} \mathbf{K})^{\top} \mathbf{s} - \mathbf{Q} \mathbf{x}_{\text{ref}} + \mathbf{P} (\mathbf{A} - \mathbf{A}_{\text{ref}}) \mathbf{x}_{\text{ref}}, \quad \mathbf{s}(t = \infty) = \mathbf{s}_{\infty}\]且 \(\mathbf{A}_{\text{ref}}\) 为参考信号的系统矩阵:
\[\dot{\mathbf{x}}_{\text{ref}}(t) = \mathbf{A}_{\text{ref}} \mathbf{x}_{\text{ref}}\]后续扩展
- 连续时间 LQR 加上不等式约束,参考 KKT。
- 离散时间 LQR 加上不等式约束,参考动态规划。
- LQR 加上高斯噪声,参考 LQG
参考资料
- 维基百科 - LQR控制器 https://zh.wikipedia.org/zh-hans/LQR控制器
