电池物理建模
Published:
第 3.2 节:固相中的电荷守恒(Charge Conservation in Solid Phase)
🎯 本节目标
我们从锂离子电池的固体部分(即电极材料)开始推导微观尺度下的控制方程。
🧠 假设前提
- 固相电极被视为均匀导电材料;
- 可以使用欧姆定律(Ohm’s Law);
- 忽略磁效应,假设电场由电势梯度决定,即 $\mathbf{E} = -\nabla \phi$。否则,$\mathbf{E} = -\nabla \phi - \frac{\partial \mathbf{A}}{\partial t}$,其中 $\mathbf{A}$ 为矢量磁势。
⚡ 欧姆定律(点形式、连续体形式)
在均匀介质中,欧姆定律为:
\[\boxed{ \mathbf{i} = \sigma \mathbf{E} = -\sigma \nabla \phi }\]其中:
- $\mathbf{i}(x, y, z, t)$:电流密度向量 [A/m²];
- $\sigma(x, y, z, t)$:导电率 [S/m],材料相关;
- $\phi(x, y, z, t)$:电势 [V];
- $\mathbf{E}(x, y, z, t)$:电场强度 [V/m],由电势梯度给出。
🔁 电荷守恒的积分形式(连续性方程 Continuity Equation)
基于电荷守恒原理(KCL 的微分形式),考虑一个有体积 $V$、边界面为 $S$ 的区域, 电流密度 $\mathbf{i}$ 指向区域内部:
\[\int_S \mathbf{i} \cdot \hat{\mathbf{n}} \, dS = - \frac{d}{dt} \int_V \rho_V \, dV\]其中:
- $\hat{\mathbf{n}}$:边界面外法向量;
- $\rho_V$:单位体积内的电荷密度(单位 C/m³);
- 负号表示“向内电流”会导致区域内电荷积累(即电荷增加);
- 电荷只能通过区域的边界流入或流出,而不能在内部产生或消灭。
🧮 微分形式(点形式)
将上式转化为微分形式(对任意体积取极限):
\[\boxed{ \nabla \cdot \mathbf{i} = -\frac{\partial \rho_V}{\partial t} }\]这就是电荷守恒的“点形式”(local conservation law)。
📉 特殊假设:稳态或电子移动极快
在锂离子电池中,电子在固体电极中的移动非常快,可以认为:
\[\frac{\partial \rho_V}{\partial t} \approx 0 \quad \Rightarrow \quad \nabla \cdot \mathbf{i} = 0\]将欧姆定律代入得:
\[\boxed{ \nabla \cdot (-\sigma \nabla \phi_s) = 0 }\]或简写为:
\[\boxed{ \nabla \cdot \mathbf{i}_s = 0 }\]其中:
- 下标 $s$ 代表固相;
- $\phi_s$:固相中的电势;
- $\mathbf{i}_s$:固相中的电流密度;
- 该方程为固相导电区域内的电荷守恒方程。
✅ 小结
- 本节推导了电极中电流连续性方程,为微观建模提供了基础;
欧姆定律 + 电荷守恒 + 快速电子假设 ⇒ 得到偏微分方程:
\[\boxed{ \nabla \cdot (-\sigma \nabla \phi_s) = 0 }\]- 它将在后续模型中用于计算固体区域的电势分布与电流流动。
第 3.3 节:固相中的质量守恒(Mass Conservation in Solid Phase)
🎯 本节目标:
推导锂离子在固体电极材料(正极或负极)中扩散的控制方程,也就是:
\[\frac{\partial c_s}{\partial t} = \nabla \cdot (D_s \nabla c_s)\]这个公式描述了:锂在电极颗粒内部的扩散行为。
背景知识:摩尔与物质的迁移
- 摩尔(mol)是描述粒子数量的单位:1 mol ≈ $6.022 \times 10^{23}$ 个粒子;
- 本节关注的是锂原子在电极颗粒中如何扩散(无对流、无电场,只考虑扩散)。
菲克定律(Fick’s Law)– 扩散的基本定律
❗ 假设:只有扩散(没有对流、反应等),且为线性介质
Fick 第一定律(点形式):
\[\boxed{ \mathbf{N} = -D \nabla c }\]其中:
- $\mathbf{N}(x,y,z,t)$:锂的摩尔通量 [mol/m²/s],表示单位时间、单位面积穿过某点的锂摩尔数;
- $D(x,y,z,t)$:扩散系数 [m²/s],反映材料对锂的扩散能力;
- $c(x,y,z,t)$:锂浓度 [mol/m³];
- $\nabla c$:浓度梯度。
说明: 通量的方向是朝向浓度降低的方向,负号表示“扩散由高浓度流向低浓度”。
连续性方程(质量守恒)
积分形式:
对某体积 $V$ 应用质量守恒:
\[\int_S \mathbf{N} \cdot \hat{\mathbf{n}} \, dS = -\frac{d}{dt} \int_V c \, dV\]- LHS 是从体积 $V$ 表面流出的通量;
- RHS 是体积 $V$ 内物质总量的变化率;
- $c$:该区域内的锂浓度。
微分形式(点形式):
通过体积缩小、除以体积并取极限,得:
\[\boxed{ \nabla \cdot \mathbf{N} = -\frac{\partial c}{\partial t} }\]即锂通量的散度决定了该点的浓度变化率。
代入菲克定律:
将 $\mathbf{N} = -D \nabla c$ 代入连续性方程:
\[\nabla \cdot (-D \nabla c) = -\frac{\partial c}{\partial t} \quad \Rightarrow \quad \frac{\partial c}{\partial t} = \nabla \cdot (D \nabla c)\]这是 扩散方程(Diffusion Equation) 的标准形式。
在固相中的表达式:
为了区分电解液与固体,给浓度和扩散系数加上下标 $s$:
\[\boxed{ \frac{\partial c_s}{\partial t} = \nabla \cdot (D_s \nabla c_s) }\]这是锂在固体电极颗粒中的质量守恒控制方程。
使用化学势的推导
在理想稀溶液中,摩尔化学势和浓度有对数关系:
\[\mu = f(c) = \mu_0 + R T \ln c\]其中
- $\mu_0$: 标准摩尔化学势,即组份在标准状态下($c = 1 \text{mol}/\text{m}^3$)的化学势 [J/mol]
- $R$: 通用气体常数
- $T$: 热力学温度(绝对温度)
等温条件下,对上式求梯度得:
\[\nabla \mu = \frac{\partial f}{\partial c} \nabla c = \frac{R T}{c} \nabla c\]因此,菲克第一定律可以表示为:
\[\mathbf{N} = -D \nabla c = -\frac{D}{\frac{\partial f}{\partial c}} \nabla \mu = - \frac{D c}{R T} \nabla \mu = - M(c) \nabla \mu\]其中 $ M(c) = \frac{D}{\frac{\partial f}{\partial c}} = \frac{D c}{R T} $ 称为迁移率(Mobility)。
菲克第二定律可以表示为
\[\frac{\partial c}{\partial t} = \nabla \cdot \left( \frac{D c}{R T} \nabla \mu \right)\]Cahn-Hilliard 方程
考虑相变问题时,摩尔化学势表示为:
\[\mu = \mu_{\mathrm{hom}}(c) - \kappa \nabla^2 c = \frac{\partial f_{\text{hom}}(c)}{\partial c} - \kappa \nabla^2 c\]其中
- $f_{\text{hom}}(c)$ 为局部自由能密度(Free Energy Density) [$\text{J/m}^3 $],描述相分离(Phase Separation);
- $\kappa$ 为梯度能系数(Gradient Energy Coefficient) [$\text{J} \cdot \text{m}^5 \cdot \text{mol}^{-2} $],描述由于浓度不均匀而导致的额外自由能惩罚;
- $-\kappa \nabla^2 c$ 项表示自动生成相界面。$\kappa$越大,界面越宽。
$f_{\text{hom}}(c)$ 通常由两部分组成:
\[f_{\mathrm{hom}}(c) = f_{\rm mix}(c) + f_{\rm int}(c)\]其中第一项为理想二元混合(ideal binary mixing)的自由能密度:
\[f_{\rm mix}(c)=RT\left[ c\ln\frac{c}{c_{\max}}+\big(c_{\max}-c\big)\ln\!\Big(1-\frac{c}{c_{\max}}\Big) \right],\]第二项为焓相互作用项,描述非理想行为:
\[f_{\rm int}(c) = \Omega\,\frac{c}{c_{\max}}\left(1 - \frac{c}{c_{\max}}\right) c_{\max}\]其中:
- $\Omega$ 为相互作用参数(Interaction Parameter)或正则溶液参数(Regular Solution Parameter),单位 $\text{J/mol}$,用来描述体系中不同组分(如锂离子与空位)之间的混合焓效应;
- 如果 $\Omega > 0$,表示组分间相互排斥(倾向于相分离);
- 如果 $\Omega < 0$,表示组分间相互吸引(倾向于均匀混合);
- 在固态电极中,这一项控制相分离驱动力,是成分梯度和相界面形成的根源之一。
$f_{\mathrm{hom}}(c)$ 对浓度求偏导得:
\[\mu_{\mathrm{hom}}(c) = \frac{\partial f_{\text{hom}}(c)}{\partial c} = RT\ln\frac{c}{\,c_{\max}-c\,} + \Omega\left(1 - 2\frac{c}{c_{\max}}\right).\]摩尔化学势为:
\[\mu = RT\ln\frac{c}{\,c_{\max}-c\,} + \Omega\left(1 - 2\frac{c}{c_{\max}}\right) - \kappa \nabla^2 c\]对上式求梯度。当 $ \kappa \neq 0 $,时得
\[\nabla \mu = \left[ R T \left( \frac{1}{c} + \frac{1}{c_{\max} - c} \right) - \frac{2 \Omega}{c_{\max}}\right] \nabla c - \kappa \nabla^3 c\]当 $ \kappa = 0 $,时,相变的界面宽度为 0,于是
\[\nabla \mu = \left[ R T \left( \frac{1}{c} + \frac{1}{c_{\max} - c} \right) - \frac{2 \Omega}{c_{\max}}\right] \nabla c\]菲克第二定律可以表示为
\[\frac{\partial c}{\partial t} = \nabla \cdot \left( D_{\rm eff}(c) \nabla c \right)\]其中
\[D_{\rm eff}(c) = D \left( \frac{c_{\max}}{c_{\max} - c} - \frac{2 \Omega c}{c_{\max}}\right)\]当 $c \ll c_{\max}$ 且 $\Omega = 0$ 时,上式退化为恒定扩散系数的菲克第二定律。
下面是一个例子,对比不同 $\Omega$ 下对应的自由能密度和摩尔化学势。
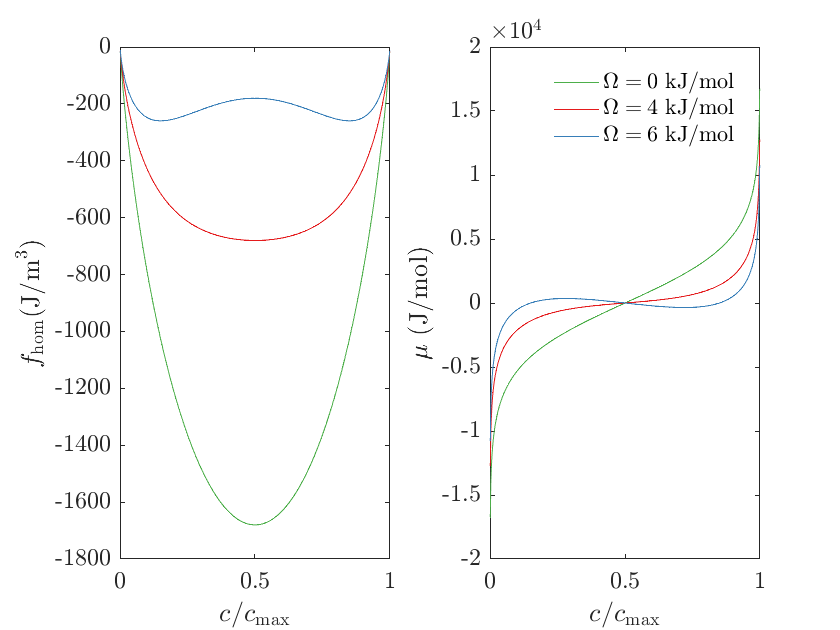
可以看到当 $\Omega = 6000$ J/mol 时,自由能密度函数是一个双井势(Double-Well Potential)函数。实际上,当 $\Omega > 2 R T$ 或者 $T < \Omega/(2 R)$ 时,双井势存在,会发生相分离。
此外,$f_{\mathrm{hom}}(c)$ 的形式保证 $c/c_{\max}$ 以 $0$ 和 $1$ 为边界,而不会超出。
电极电势
电势 $\phi$ 与电化学势的关系如下
\[\mu(c) = \mu_0 + {z F} \phi = \mu_0 + {F} \phi\]其中对于锂离子电池 $ z = 1$,$\mu_0 $ 为参考电化学势,实验测定的电极电势为
\[U(c) = \phi(c) + \phi_{\text{ref}} = \frac{ \mu(c) - \mu_0 }{F} + \phi_{\text{ref}}\]其中 $\phi_{\text{ref}} $ 为参考电势。锂离子电池中,选取 $\text{Li/Li}^+$ 参考电极的电势为参考电势,则 $\phi_{\text{ref}} = 0$。在这个参考电极中,在平衡状态下,金属锂与溶液中锂离子的电化学势相等。
因此:
\[U(c) = \frac{ \mu(c) - \mu_0 }{F}\]利用实验测定的 $U(c)$ 数据可以拟合得到模型参数 $\mu_0$,$\Omega$,$c_{\max}$。
直接利用 $U(c)$ 修正菲克第二公式:
\[\mu(c) = F U(c) + \mu_0\]计算梯度
\[\nabla \mu = F \frac{\partial U(c)}{\partial c} \nabla c\]菲克第二定律可以表示为
\[\frac{\partial c}{\partial t} = \nabla \cdot \left( \frac{D c F}{R T} \frac{\partial U(c)}{\partial c} \nabla c \right)\]可记
\[D_{\rm eff}(c) = \frac{D c F}{R T} \frac{\partial U(c)}{\partial c} = M(c) F \frac{\partial U(c)}{\partial c}\]重要备注
相分离/自旋odal 区:若 $\partial U/\partial c<0\Rightarrow \partial \mu/\partial c<0$,上式给出 $D_{\rm eff}<0$,出现“上坡扩散”。这时Fick 形式失效,应使用 Cahn–Hilliard:
\[\frac{\partial c}{\partial t} =\nabla\!\cdot\!\Big(\frac{D}{RT}\,c\,\nabla[\mu_{\rm hom}(c)-\kappa\nabla^2 c]\Big).\]参考点常数不会影响导数 $\partial \mu/\partial c$,因此不会影响 $D_{\rm eff}$。
另一种量纲
文献中常见的另一种化学势的量纲和能量相同。将摩尔化学势除以 $F/e$ 得:
\[\tilde{\mu} = k_B T\ln\frac{c}{\,c_{\max}-c\,} + \tilde{\Omega} \left(1 - 2\frac{c}{c_{\max}}\right) - \tilde{\kappa} \nabla^2 c\]其中
- $k_B = Re/F = 1.381 \times 10^{-23}~[\text{J/K}]$ 为玻尔兹曼常数;
- $F = 96485~[\text{C/mol}]$ 为法拉第常数;
- $e = 1.602 \times 10^{-10}~[\text{C}]$ 为基本电荷;
- $\tilde{\Omega} = \Omega~e/F$,单位 [$\text{J}$]
- $\tilde{\kappa} = \kappa~e/F$,单位 [$\text{J} \cdot \text{m}^5 \cdot \text{mol}^{-1} $]
对比电荷与质量的连续性方程
| 电荷守恒 | 质量守恒 | 解释 |
|---|---|---|
| $\mathbf{i}_s = - \sigma \nabla \phi_s$ | $\mathbf{N} = -D_s \nabla c_s$ | 欧姆定律 ↔ 物质扩散 |
| $\nabla \cdot \mathbf{i}_s = - \frac{\partial \rho_V}{\partial t} = 0$ | $\nabla \cdot \mathbf{N} = - \frac{\partial c}{\partial t}$ | 电荷守恒 ↔ 质量守恒 |
| $\frac{\partial \rho_V}{\partial t} = \nabla \cdot (\sigma \nabla \phi_s) = 0$ | $\frac{\partial c_s}{\partial t} = \nabla \cdot (D_s \nabla c_s)$ | 泊松方程 ↔ 菲克第二定律 |
第 3.5 节:Nernst-Planck 方程
回顾菲克第一定律的一种表示:
\[\mathbf{N} = - \frac{D c}{R T} \nabla \mu\]注意在前文中,$ \nabla \mu $ 是微观尺度化学势梯度,在局部没有电场影响。宏观尺度中我们考虑电化学势。考虑正则溶液(没有相变):
\[\mu = \mu_0 + R T \ln c + z F \phi\]带入得
\[\mathbf{N} = - D \nabla c - \frac{D z F }{R T} c \nabla \phi = - D \nabla c + \frac{D z e }{k_B T} c \mathbf{E}\]此式连同连续性方程一起被称为能斯特-普朗克(Nernst-Planck)方程。其中第一项代表扩散,第二项代表电磁迁移。注意电解液里通常不存在相变,因此不使用 Cahn-Hillard 方程来表示化学势。


